Kernelized Normalizing Constant Estimation: Bridging Bayesian Quadrature and Bayesian Optimization
Xu caiが第一著者 In this paper, a normalizing constant on RKHS is considered as follows: Z(f)=∫De−λxdx,λ>0 Z(f) = \int_{D} e^{- \lambda x} dx, \quad \lambda > 0 Z(f)=∫De−λxdx,λ>0 This method considers the lower bound and the upper bound of f∈RKHS f \in RKHS f∈RKHS This method considers the noiseless setting and the noisy setting for the lower bound of f, respectively. Applicable to a multi-layer perception, a point spread function. So authors conducted experiments with various f. Then consider the results with these experiments.
Xu caiが第一著者
In this paper, a normalizing constant on RKHS is considered as follows:
Z(f)=∫De−λxdx,λ>0
Z(f) = \int_{D} e^{- \lambda x} dx, \quad \lambda > 0
Z(f)=∫De−λxdx,λ>0
This method considers the lower bound and the upper bound of
f∈RKHS
f \in RKHS
f∈RKHS
This method considers the noiseless setting and the noisy setting for the lower bound of f, respectively.
Applicable to a multi-layer perception, a point spread function.
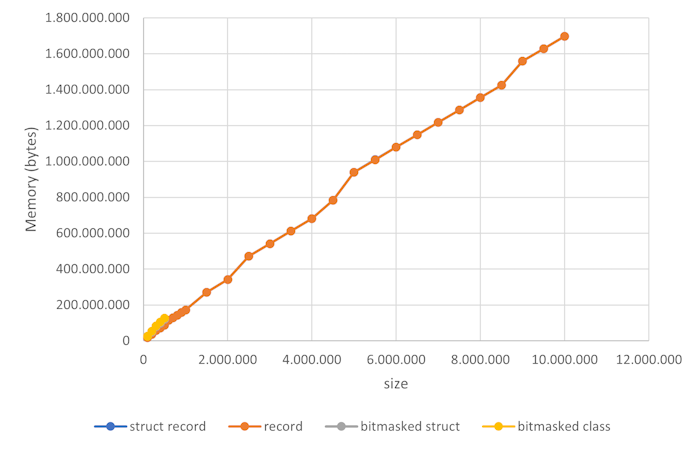
So authors conducted experiments with various f.
Then consider the results with these experiments.
