Regreso al número 42

En mi anterior entrada del Cuaderno de Cultura Científica titulada Sobre el interesante juego matemático que nos plantea Alicia con la tabla de multiplicar del cuatro  estuvimos explicando unas curiosas y extrañas multiplicaciones que se mencionaban en Las aventuras de Alicia en el País de las Maravillas (1865), de Lewis Carroll, las cuales tenían una pequeña relación con el número 42, un número por el que aparentemente tenía una cierta predilección el matemático británico Charles L. Dodgson (1832-1898), que todos conocemos por su seudónimo, Lewis Carroll. Vamos a dedicar la presente entrada a este sencillo, pero bastante popular, número, el cuarenta y dos (42).

El número 42 en el País de las Maravillas

El origen del famoso libro Las Aventuras de Alicia en el País de las Maravillas se remonta a cierta tarde del mes de julio de 1862 cuando el matemático británico Charles L. Dodgson, profesor de matemáticas en el Christ Church College de la Universidad de Oxford y ministro de la Iglesia Anglicana, junto al reverendo Robinson Duckworth, miembro del consejo rector del Trinity College, también de la Universidad de Oxford, llevaron de excursión en barca por el río Támesis a las tres hermanas Liddell, Alice, de 10 años, Lorina, de 13 años, y Edith, de 8 años, que eran hijas del decano del Christ Church College, Henry G. Liddell. Durante dicha excursión por el Támesis Charles Dodgson se inventó un cuento sobre una niña llamada Alicia que vivió una curiosa aventura bajo tierra y que encantó a las tres hermanas. Este fue uno de muchos cuentos que, según Dodgson, les contó a las tres niñas en diferentes excursiones, pero el cuento de ese día tuvo un final diferente, ya que la joven Alicia Liddell le pidió a su autor que lo escribiera. Dos años más tarde, en noviembre de 1864, Charles Dodgson le dio a Alicia Liddell el manuscrito que había escrito, cuyo título era Las aventuras de Alicia bajo tierra y que había ilustrado el propio autor.

Charles Dodgson, animado por los novelistas y amigos Henry Kingsley (1830-1876) y George MacDonald (1824-1905), quien se lo había leído a sus hijos, decidió publicar el cuento sobre esa niña llamada Alicia que se aburría y acabó viviendo una extraña aventura bajo tierra. Dodgson añadió nuevo material, como la carrera loca, el gato de Cheshire, la transformación del bebé en cerdo, la fiesta del té del Sombrerero loco o una parte importante del juicio, algunas de las cuales tienen alusiones ocultas a cuestiones matemáticas. Espero escribir sobre estas cuestiones en alguna futura entrada. Aunque la cita de las extrañas multiplicaciones “cuatro por cinco son doce; cuatro por seis, trece; cuatro por siete … ¡Dios mío, de esta manera no llegaré nunca a veinte!”, a la que dediqué mi anterior entrada, sí estaba en el manuscrito original.

Aunque en el manuscrito original las ilustraciones eran del propio Dodgson, para la publicación del mismo acabó recurriendo al ilustrador británico John Tenniel (1820-1914), que era el dibujante y caricaturista de la revista de humor y sátira Punch. La publicación definitiva estaba formada por 42 ilustraciones de Tenniel. Y aquí tenemos una presencia del número 42 en Las aventuras de Alicia en el País de las Maravillas, que es como terminó titulándose el libro cuya primera edición fue publicada en noviembre de 1865, firmada por Lewis Carroll, seudónimo que Charles Dodgson utilizaba desde 1856, cuando hizo uso del mismo para su poema Soledad, publicado en la revista literaria The train.

Pero vayamos con más referencias al número 42. En el último capítulo del libro, el capítulo XII, durante el juicio, puede leerse el siguiente pasaje en el que se menciona la regla 42.

 

En este momento el Rey, que durante un rato había estado escribiendo febrilmente en su cuaderno de notas, gritó:

 

– ¡Silencio! –y leyó en voz alta: “Regla Cuarenta y Dos. Todas las personas que midan más de una milla [de altura] habrán de abandonar la sala”.  

 

Todo el mundo miró a Alicia.

 

– Yo no mido una milla –dijo Alicia.

 

– Sí la mides –dijo el Rey.

 

– Casi dos millas –añadió la Reina.

 

– Bueno, de todos modos, no me iré –dijo Alicia–; además, esa no es una regla general: la acabáis de inventar.

 

– Es la regla más antigua del libro –dijo el Rey.

 

– Entonces debería ser la Número Uno.

 

Por otra parte, en el inicio del libro Las aventuras de Alicia en el País de las Maravillas, su protagonista Alicia ve un curioso conejo blanco con chaleco y reloj de bolsillo al que oye decir “¡Dios mío! ¡Dios mío! ¡Voy a llegar demasiado tarde!” y sin pensárselo dos veces le sigue cuando este entra en su madriguera. Nada más entrar Alicia empieza a caer y sigue cayendo, y cayendo. Y podemos leer el siguiente pasaje.

 

Siguió cayendo, cayendo, cayendo. ¿Es que la caída nunca iba a tener fin? “Me pregunto cuántas millas llevaré ya”, dijo en voz alta. “Debo de estar ya cerca del centro de la Tierra. Veamos: el centro estará a unas cuatro mil millas, creo…” (como veis, Alicia había aprendido varias cosas de este tipo en el colegio, y aunque no era muy buena ocasión para presumir de lo que sabía, ya que no había nadie que la escuchase, sin embargo, era buena práctica repetirlo) “… sí, creo que es esa la distancia… Pero entonces, ¿en qué latitud y longitud me encuentro?” (Alicia no tenía la menor idea de lo que eran latitud y longitud, pero le pareció que eran palabras importantes).

 

Luego empezó otra vez: “¡No sé si atravesaré el centro de la Tierra de parte a parte en la caída! ¡Qué divertido sería aparecer entre la gente que anda cabeza abajo! Los antípatas, creo…” (casi se alegró de que no hubiese nadie escuchando esta vez, ya que no le sonó correcta la palabra, ni mucho menos)…

 

Como comenta el divulgador estadounidense Martin Gardner en su libro Alicia anotada (1960), en los tiempos de Lewis Carroll / Charles Dodgson se especuló mucho sobre lo que sucedería si alguien, o un objeto, cayese por un agujero que pasara por el centro de la Tierra. Sobre esta cuestión, que ya se había estudiado desde la antigüedad, el matemático y astrónomo italiano Galileo Galilei (1564-1642) obtuvo la solución: el objeto caería a velocidad creciente, pero con aceleración decreciente hasta llegar al centro de la Tierra, momento en que la aceleración sería cero; a partir de ahí su velocidad disminuiría al aumentar su desaceleración, hasta alcanzar la abertura en el otro extremo; entonces volvería otra vez hacia atrás. Si se ignorasen la resistencia del aire y la fuerza de coriolis, el objeto se desplazaría de manera infinita entre ambos extremos de la Tierra.

Según el matemático británico Edward Wakeling (1946-2023), quien fuera tesorero, secretario y presidente de la Lewis Carroll Society, en su artículo Further findings about the number forty two / Más hallazgos sobre el número cuarenta y dos, publicado en la revista Jabberwocky de la Lewis Carroll Society en 1988, es bastante probable que Charles Dodgson hubiese calculado el tiempo que habría tardado una piedra, lanzada por un agujero (el de la madriguera del conejo) que pasase por el centro de la tierra, en llegar al otro lado del mundo, unos 42 minutos (existen muchos artículos y blogs donde se hace este cálculo, por ejemplo, Viaje por el interior de la Tierra, los artículos Through the Earth in Forty Minutes, del físico Paul W. Cooper, publicado en la American Journal of Physics, en 1966, y The Answer Is Forty-Two — Many Mechanics Problems, Only One Answer, del físico Robert H. Romer, publicado en The Physics Teacher, en 2003, o la entrada de la Wikipedia sobre el Gravity Train / Tren gravitacional).

El número 42 no aparece directamente en el fragmento sobre la tabla de multiplicar del cuatro que habíamos comentado, “cuatro por cinco son doce; cuatro por seis, trece; cuatro por siete … ¡Dios mío, de esta manera no llegaré nunca a veinte!”, pero sí de forma indirecta como se explicó en la entrada Sobre el interesante juego matemático que nos plantea Alicia con la tabla de multiplicar del cuatro, donde podéis leer la explicación y algunas cosas más.

En la continuación de Las aventuras de Alicia en el País de las Maravillas, titulada A través del espejo y lo que Alicia encontró allí (1871), también se puede encontrar alguna referencia al número 42. El número total de soldados y caballos que envió el Rey Blanco en apoyo de Tentetieso (Humpty Dumpty) es de 4207, número en el que tenemos el deseado número 42, así como uno de sus factores primos, el 7.

Por otra parte, en el capítulo V, se produce la siguiente conversación entre la Reina Blanca y Alicia.

 

– Consideremos tu edad para empezar: ¿Cuántos años tienes?

 

– Siete y medio exactamente.

 

– No hace falta que digas “exactamente” –comentó la Reina–. Puedo creerlo sin necesidad de eso. Y ahora te propongo algo que creer. Yo tengo ciento un años, cinco meses y un día.

 

– ¡Eso no lo puedo creer! –dijo Alicia.

 

A partir de esta cita, Edward Wakeling, en el artículo mencionado anteriormente, hace una estimación de los días que ha vivido la Reina Blanca, teniendo en cuenta que la historia de Alicia a través del espejo y lo que allí encontró empezaría el 4 de noviembre de 1859, de 37.044 días. Además, supone que la Reina Roja podría tener la misma edad, luego entre ambas habrían vivido 74.088 días, que son 42 x 42 x 42 días (42 al cubo). Además, la edad de Alicia es 7 años y 6 meses, de manera que, si multiplicamos ambos números, 6 x 7, nos da 42.

Más sobre el número 42 en Lewis Carroll

Pero no terminan aquí las referencias al número 42 en la obra de Lewis Carroll. Por ejemplo, en el surrealista poema La caza del Snark (ya comentamos un fragmento del mismo, relacionado con los mapas, en la entrada del Cuaderno de Cultura Científica titulada El mapa Dymaxion), publicado en 1876, también aparece una mención al número 42. En el inicio del poema, en el Espasmo I (El desembarco), cuando se está describiendo a la tripulación mientras desembarca, podemos leer lo siguiente.

 

Había uno que era famoso por el número de cosas

que se había olvidado al subir al barco:

su paraguas, su reloj, todas sus joyas y anillos,

y la ropa que había comprado para el viaje.

  

Tenía cuarenta y dos cajas, empaquetadas con gran cuidado,

con su nombre escrito claramente en ellas,

pero, como se le olvidaron,

todas se quedaron en la playa.

 

La pérdida de sus ropas no importaba casi nada, porque

cuando llegó al barco llevaba puestos siete abrigos

y tres pares de botas. Sin embargo, lo peor era

que había olvidado totalmente su nombre.

También hay una mención al número 42 en su poema Fantasmagoría (1869), que es una conversación entre un hombre de mediana edad, dueño de una casa, y un pequeño fantasma, con poca experiencia en las artes de asustar, que visita la casa del hombre y le explica al mismo las reglas básicas para los seres que como él se dedican a asustar.

Por derecho, los espectros eligen los primeros,

a la hora de cubrir una vacante.

Luego, los fantasmas, los elfos, las hadas y los duendes…

Y si todos éstos fallan, se invita

al espíritu necrófago más simpático que se encuentre.

 

Los espectros dijeron que el lugar era humilde

y que usted guardaba un vino muy malo.

Así que tuvo que venir un fantasma

y, como yo era el primero, ya sabe,

no pude negarme.

 

«Sin duda», dije, «eligieron

al mejor que podían enviar,

¡Aunque elegir a un mocoso como tú

para visitar a un hombre de cuarenta y dos,

no ha sido un gran detalle!»

La respuesta definitiva a la vida, el universo y todo lo demás

Aunque, sin lugar a dudas, la mención más conocida sobre el número 42 es la que realiza el escritor inglés Douglas Adams (1952-2001) en La guía del autoestopista galáctico, una serie clásica de novelas de ciencia ficción de la década de los años 1980. La serie literaria se compone de cinco libros, el primero que da título a toda la serie, La guía del autoestopista galáctico, fue publicado en 1979, al que siguieron El restaurante del fin del mundo; La vida, el universo y todo lo demás; Hasta luego, y gracias por el pescado e Informe sobre la Tierra.

En la novela aparece un superordenador, llamado Pensamiento Profundo y que es el segundo ordenador más grande del universo del espacio y del tiempo, que ha sido construido por una raza de seres “pan-dimensionales” que buscan el sentido de la vida. Cuando le preguntan al superordenador cuál es la “respuesta definitiva a la vida, el universo y todo lo demás”, éste contesta, después de siete millones y medio de años haciendo cálculos, que “cuarenta y dos”.

 

    – Buenos días –dijo al fin Pensamiento Profundo.

 

    – Hmmm… Buenos días, Pensamiento Profundo –dijo nerviosamente Loonquawl–, ¿tienes… hmmm, es decir…?

 

    – ¿Una respuesta que daros? –le interrumpió Pensamiento Profundo en tono majestuoso–. Sí, la tengo.

 

    Los dos hombres temblaron de expectación. Su espera no había sido en vano.

 

    – ¿De veras existe? –jadeó Phouchg.

 

    – Existe de veras –le confirmó Pensamiento Profundo.

 

    – ¿A todo? ¿A la gran pregunta de la Vida, del Universo y del Todo?

 

    – Sí.

 

    Los dos hombres estaban listos para aquel momento, se habían preparado durante toda la vida; se les escogió al nacer para que presenciaran la respuesta, pero aun así jadeaban y se retorcían como criaturas nerviosas.

 

    […] Los dos hombres se agitaron inquietos. La tensión era insoportable.

 

    – En serio, no os va a gustar –observó Pensamiento Profundo.

 

    – ¡Dínosla!

 

    – De acuerdo –dijo Pensamiento Profundo–. La Respuesta a la Gran Pregunta…

 

    – ¡Sí…!

 

    – … de la Vida, del Universo y de Todo… –dijo Pensamiento Profundo.

 

    – ¡Sí…!

 

    – Es… –dijo Pensamiento Profundo, haciendo una pausa.

 

    – ¡Sí…!

 

    – Es…

 

    – ¡¡¡¿Sí…?!!!

 

    – Cuarenta y dos –dijo Pensamiento Profundo, con calma y majestad infinitas.

Después de la aparición del número 42 en la serie de novelas La guía del autoestopista galáctico, se hizo muy popular dentro de la “comunidad friki”, lo que ha provocado que sigan apareciendo referencias al mismo. Por ejemplo, en la novela La anomalía (2021), del escritor francés Hervé Le Tellier, existe un Protocolo 42, cuyo nombre se lo pone un matemático friki que siente devoción por la serie de novelas de Douglas Adams.

Aunque hay quienes afirman que el escritor Douglas Adams se inspiró en Lewis Carroll para elegir el número 42, el autor de La guía del autoestopista galáctico afirmó que no había nada especial en la elección de ese número.

Era una broma. Tenía que ser un número, un número normal y pequeño, y lo elegí. Las representaciones binarias, la base trece y los monjes tibetanos son tonterías. Me senté en mi escritorio, miré al jardín y pensé: «42 bastará». Lo tecleé. Fin de la historia.

Un poco de matemáticas para el número 42

Para terminar esta entrada vayamos con algunas propiedades matemáticas del número 42. Es un número no primo (es par), producto de tres primos 2, 3 y 7 (es lo que se denomina un primo esfénico, 42 = 2 x 3 x 7), que se encuentra en medio de dos primos gemelos, 41 y 43.

Además, es un número abundante (véase la entrada Los números enamorados) puesto que el número (42) es menor que la suma se sus divisores propios (1 + 2 + 3 + 6 + 7 + 14 + 21 = 54). Más aún, es un número abundante primitivo, ya que ninguno de sus divisores propios es un número abundante (por ejemplo, 14 no es abundante, ya que 14 es mayor que 1 + 2 + 7 = 10). Más aún, es un número admirable ya que, aunque la suma de los divisores propios no es el propio número (propiedad característica de una familia importante de números naturales, los denominados números perfectos), sí es igual a la suma de los divisores propios, pero uno de ellos con signo menos (es decir, resta), 42 = 1 + 2 + 3 – 6 + 7 + 14 + 21.

Siguiendo con los divisores, podemos decir que el número 42 es un número práctico (sobre ellos también hablamos en la entrada Los números enamorados) ya que todos los números menores que él, desde el 1 al 41, pueden ser expresados como suma de algunos de los divisores de 42. Veámoslo. Los divisores de 42 son 1, 2, 3, 6, 7, 14 y 21, luego

1 = 1, 2 = 2, 3 = 3, 4 = 1 + 3, 5 = 2 + 3, 6 = 6, 7 = 7, 8 = 1 + 7, 9 = 2 + 7, 10 = 3 + 7, 11 = 1 + 3 + 7, 12 = 1 + 2 + 3 + 6, 13 = 6 + 7, 14 = 14, 15 = 1 + 14, 16 = 2 + 14, 17 = 3 + 14, 18 = 1 + 3 + 14, 19 = 2 + 3 + 14, 20 = 6 + 14, 21 = 21, 22 = 1 + 21, 23 2 + 21, 24 = 3 + 21, 25 = 1 + 3 + 21, 26 = 2 + 3 + 21, 27 = 6 + 21, 28 = 7 + 21, 29 = 1 + 7 + 21, 30 = 2 + 7 + 21, 31 = 3 + 7 + 21, 32 = 1 + 3 + 7 + 21, 33 = 2 + 3 + 7 + 21, 34 = 6 + 7 + 21, 35 = 14 + 21, 36 = 1 + 14 + 21, 37 = 2 + 14 + 21, 38 = 3 + 14 + 21, 39 = 1 + 3 + 14 + 21, 40 = 2 + 3 + 14 + 21, 41 = 6 + 14 + 21.

Por otra parte, el número 42 es un número harshad, o de Niven, ya que es divisible por la suma de sus dígitos, 4 + 2 = 6 (para saber más sobre los números harshad puede consultarse la entrada Los números que proporcionan alegría).

El número 42 se puede escribir como suma de números naturales consecutivos

42 = 3 + 4 + 5 + 6 + 7 + 8 + 9,

lo que hace que el 42 pertenezca a la familia de los números corteses, o trapezoidales.

El número 42 pertenece a otra familia muy importante de números naturales, los números de Catalan (véase el libro La gran familia de los números). Es una de las familias más importantes de la combinatoria, que fue descrita por primera vez por el matemático Leonhard Euler, quien estaba interesado en el problema de contar las distintas formas en las que un polígono convexo de n lados puede dividirse en triángulos mediante diagonales que no se cruzan. La solución son los números de Catalan 1, 2, 5, 14, 42, 132, 429…

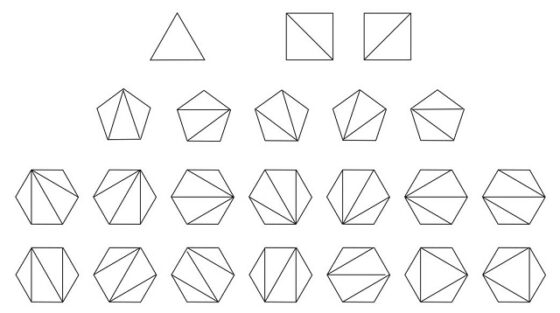
Y existen 42 formas distintas de dividir un heptágono en triángulos mediante diagonales que no se cruzan, como se muestra en la imagen.

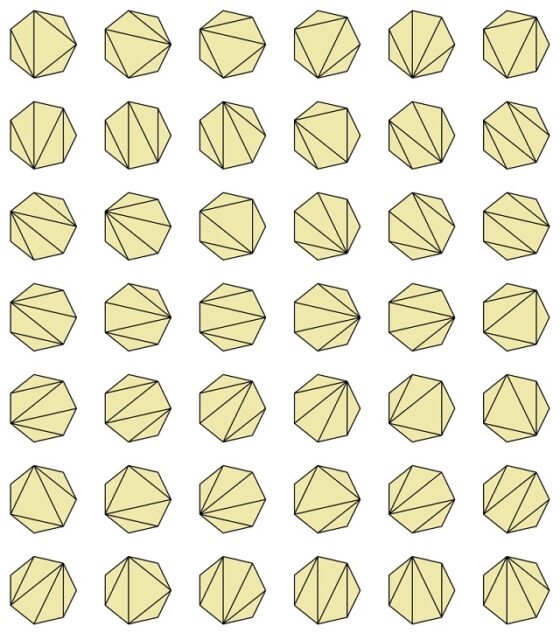
El nombre de esta familia se debe al matemático francobelga Eugène Charles Catalan (1814-1894), quien demostró una fórmula, conjeturada por Euler, que expresa estos números en función de los números combinatorios.

Los números de Catalan se pueden describir de formas muy distintas, pero no dedicaremos esta entrada a este tema, ya volveremos sobre el mismo en alguna entrada futura.

Para terminar, decir que el número 42 puede escribirse como la suma de tres cubos de números enteros de la siguiente forma

Esta no es una cuestión sencilla. De hecho, el problema diofántico de escribir los 100 primeros números naturales como suma de tres cubos de números enteros, que se planteó en 1955, no fue resuelto completamente hasta septiembre de 2019, cuando se publicó el último de los números que faltaba, que no era otro que el número 42 (en la entrada 42, la respuesta definitiva a la vida, el universo y todo lo demás podéis leer todos los detalles sobre la reslución de este problema diofántico).

Bibliografía

1.-Página web Alice-in-wonderland.net: Alice-in-wonderland.net 

2.- Lewis Carroll, Alicia anotada: 150 aniversario, Edición de Martin Gardner, actualización de Mark Burstein, Akal, 2017.

3.- Raúl Ibáñez, La gran familia de los números, Libros de la catarata, 2021.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Regreso al número 42 se ha escrito en Cuaderno de Cultura Científica.