Formeln [Mathlog]
Sie sind promovierter Mathematiker. Haben zu viele Finanzexperten Formeln für Naturgesetze gehalten? Ja.Verantwortlich ist die falsch verstandene Sucht der Menschen nach Sicherheit. Bandbreiten haben nicht gereicht. Es musste immer eine genaue Zahl sein. Allianz-Deutschland-Chef Gerhard Rupprecht im Interview mit dem stern, 2. Juni 2009 Schöne Formeln „Zehn der beeindruckendsten mathematischen Formeln der Mathematik“ werden in…
![Formeln [Mathlog]](http://img.youtube.com/vi/uTn5av4VS5E/0.jpg)
Sie sind promovierter Mathematiker. Haben zu viele Finanzexperten Formeln für Naturgesetze gehalten?
Ja.Verantwortlich ist die falsch verstandene Sucht der Menschen nach Sicherheit. Bandbreiten haben nicht gereicht. Es musste immer eine genaue Zahl sein.
Allianz-Deutschland-Chef Gerhard Rupprecht im Interview mit dem stern, 2. Juni 2009
Schöne Formeln
„Zehn der beeindruckendsten mathematischen Formeln der Mathematik“ werden in einem YouTube-Video auf
erläutert.
Obwohl die Ersteller von „Echt Einfach TV“ offensichtlich auf Schulmathematik spezialisiert sind, haben sie für dieses Video (mit Ausnahme des Satzes von Pythagoras) durchgängig Formeln aus der “höheren” Mathematik ausgewählt:
1. Die Eulersche Identität
2. Das Euler-Produkt
3. Das gaußsche Fehlerintegral
4. Die Mächtigkeit des Kontinuums
5. Die Analytische Fortsetzung der Fakultät
6. Der Satz des Pythagoras
7. Die explizite Formel für die Fibonacci-Folge
8. Das Basler Problem
9. Die Harmonische Reihe
10. Die explizite Formel für die Primzahlzählfunktion
Die explizite Formel in Punkt 10 ist
Stokes‘ Formel
Eine Formel, die im Video nicht vorkommt, ist die Stokes-Formel. Das ist eine sehr einfach aussehende Formel, die wichtige Sätze aus der Elektrodynamik wie den Rotationssatz
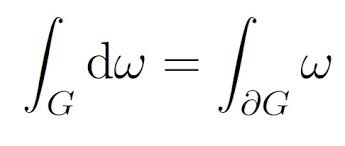
In Wirklichkeit ist die Formel nur scheinbar einfacher als die beiden obenstehenden; man muss erst wissen, was das d in der Formel bedeutet und was eine Differentialform ist und wie man sie integriert.
Die Stokes-Formel ist die Heldin eines bisher leider nur auf Französisch erschienenen Romans von Michèle Audin. Aus diesem kann man lernen, dass die Formel in dieser einfachen Form auf Georges de Rham zurückgeht, der als Lehrer in Lausanne arbeitete und in den Ferienmonaten Seminare in Paris besuchte, während er an einer Dissertation bei Lebesgue arbeitete. Letzterem gelang es, de Rham einen Termin bei Cartan in dessen Haus zu besorgen, wo er – angeblich zum Klang des Klavierspiels der übenden Cartan-Kinder – diesen von seinem Ansatz zu überzeugen vermochte. So jedenfalls die Geschichte, wie sie im Roman unter dem Datum “17. April 1930” erzählt wird.
Eine Besonderheit von Audins Roman ist, dass seine “Handlung” sich nicht chronologisch entwickelt, sondern nach Daten Monat-Tag geordnet ist, womit die Jahre (im Wesentlichen zwischen 1825 und 1936) wild durcheinandergehen. Der Roman beginnt also am 1.Januar 1862 mit dem Tod Ostrogradskis (und einigen Anekdoten über dessen späteres Erscheinen auf sowjetischen Briefmarken und Streichholzschachteln), von dem eine Variante des Gaussschen Integralsatzes stammt, und endet am 23. Dezember 1935 mit dem Erscheinen des ersten unter dem Namen Nicolas Bourbaki veröffentlichten Artikels und der Vorgeschichte des für diese Publikation benötigten Vornamens. (Die Stokes-Formel erschien in den Elementen Bourbakis erst 1971, nachdem Henri Cartan ihr aber schon 1951 einen Vortrag im Bourbaki-Seminar gewidmet hatte.)
Die nicht-chronologische Entwicklung erlaubt das Bewerten vieler nur lose mit dem Thema zusammenhängender politischer und wissenschaftlicher Ereignisse sowie das Erzählen vieler Anekdoten ohne auf eine Rahmenhandlung Rücksicht nehmen zu müssen. Und es erlaubt dem Leser an einer beliebigen Stelle einzusteigen, eine oder mehrere Seiten zu lesen und dann zu einer Stelle zu springen. (Querverweise sind zahlreich angegeben.)
Einige Male gibt es zwischendurch auch Flashforwards in die Gegenwart der Autorin, etwa am 12. April 2012 ein Telefonat mit einem Verleger: “Ich habe ihnen vor drei Monaten ein Buchprojekt geschickt und sie haben noch nicht geantwortet.” “Was war das nochmal gewesen?” “Ein Buch über die Stokes-Formel.” “Ach ja, jetzt erinnere ich mich. Nein.” “Was nein?” “Das geht nicht. Hören sie! Sie beginnen damit, den Tod eines Unbekannten zu erzählen. Danach quälen sie uns über Seiten mit langweiligen Versammlungen vergessener Mathematiker. Wer, glauben sie, wird sich für diese Typen interessieren?…”
Tatsächlich haben viele Geschichten mit der Pariser Akademie und ihren Sitzungen zu tun, deren Akten (neben anderen zur französischen Mathematikgeschichte) die Autorin für andere Buchprojekte ausgewertet hatte, so dass dieses Buch dann wohl auch dem Zweck diente, die nicht in wissenschaftlich-historischen Texte fassbaren subjektiven Teile der Geschichte eben als Roman zu verarbeiten. Auch wenn es meist um das Leben einzelner Mathematiker geht, lernt man viel über die Geschichte (nicht nur der Wissenschaft) Frankreichs und sogar einiges über Mathematik. (Man kann die stets sehr kurzen Ausführungen zur Mathematik aber auch problemlos überspringen ohne im Lesefluss gestört zu werden.)
Formeln als Design-Elemente
Die Schönheit der Stokes-Formel besteht vor allem darin, dass sie verschiedene kompliziertere Formeln in einem griffigen „Schlagwort“ zusammenfasst, so dass man sie auch als Designelement für T-Shirts, Kaffeetassen oder Tragetaschen verwenden kann.
Formeln als Designelemente sieht man nach meinem Eindruck heute häufiger als früher. Inzwischen werden sie auch schon als Signaturen verwendet. 432500 Dollar bei einer Auktion erzielte 2018 das von einer KI gezeichnete Bild „Portrait of Edmond de Belamy“, für das die KI als Signatur eine Formel wählte, die wohl aus der Theorie der „Generative Adversarial Networks“ stammt. Es handelt sich um ein Minimaxprinzip,
Eindruck schinden mit Formeln
Wer seine Artikel mit zusammenhanglosen mathematischen Formeln aufpeppt, der wird unter Geisteswissenschaftlern mehr Eindruck schinden als unter Mathematikern. Gewußt haben wir das schon immer, es lässt sich aber auch mit Zahlen und Diagrammen beweisen: In “The nonsense math effect” (erschienen in: Judgment and Decision Making , Volume 7 , Issue 6 , November 2012 , pp. 746 – 749) berichtete Kimmo Eriksson über folgendes Experiment: 200 Hochschulabsolventen unterschiedlicher Fächer bekamen Zusammenfassungen zweier Artikel aus Fachzeitschriften vorgelegt – im einen Artikel ging es darum, wie australische Eingeborene ihre gefangenen Fische untereinander aufteilen, der andere Artikel untersuchte, ob vorbestrafte Schwarze auf dem Arbeitsmarkt gegenüber vorbestraften Weißen benachteiligt werden – und sollten deren wissenschaftlichen Anspruch vergleichend beurteilen. Der Witz: in jeweils eine der beiden Zusammenfassungen wurde folgender Satz eingebaut:
A mathematical model (TPP=T0−fT0df2−fTPdf) is developed to describe sequential effects.
Der Satz machte im jeweiligen Zusammenhang natürlich keinerlei Sinn, weder ging es in den Arbeiten um Sequenzmodelle noch kamen Variablen TP, df etc. vor.
Das Ergebnis: Absolventen natur- und technikwissenschaftlicher Studiengänge bewerteten die Arbeit mit der Nonsens-Formel eher negativ (aber auch nur zu 54%), Absolventen anderer Studiengänge aber überwiegend positiv: Mediziner zu 64%, Geistes- und Sozialwissenschaftler zu 62% und andere (vor allem Erziehungswissenschaftler) zu 73%.
The experimental results suggest a bias for nonsense math in judgments of quality of research. Further, this bias was only found among people with degrees from areas outside mathematics, science and technology. Presumably lack of mathematical skills renders difficult own critical evaluation of meaningless mathematics.
Zölle
Die unten abgebildete Formel diente Anfang April zur Berechnung der neuen Zölle eines Landes bei Einfuhren in die USA. Dabei bezeichnete
Epsilon und phi sind Konstanten, deren ursprüngliche Bedeutung ich vergessen habe. Allerdings wurde bei den Berechnungen pauschal phi gleich 1/4 und epsilon gleich 4 gesetzt, womit sich epsilon und phi wegheben und eigentlich auch weggelassen werden könnten. Es ging wohl nur darum, dass eine Formel mit griechischen Buchstaben mehr hermacht. Und von der Einfachheit der Formel ablenkt.
Statt strategische Sektoren zu identifizieren, schaut Trump vor allem auf die Handelsüberschüsse der jeweiligen Länder im Warenverkehr. Doch will der Mann im Weißen Haus wirklich, dass Amerikaner künftig für den Sportartikelhersteller Nike Turnschuhe nähen?
kommentierte Spiegel Online.




















:quality(80)/p7i.vogel.de/wcms/76/3a/763a715e66cae0a4c172ab9002440ee8/0124301761v1.jpeg?#)









































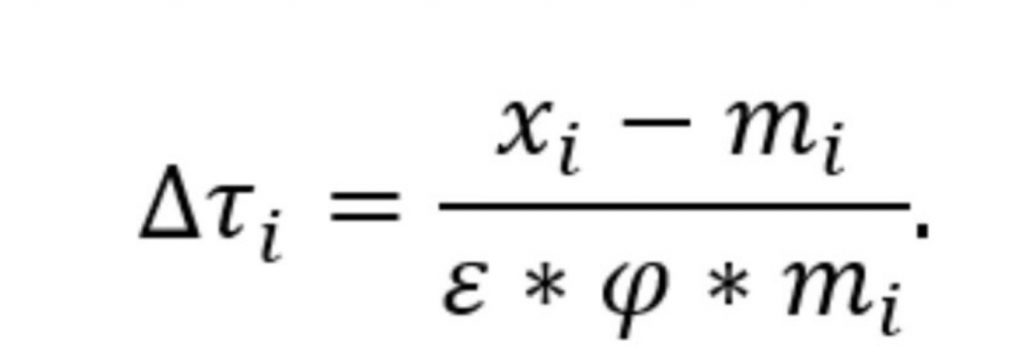
![Auf Reisen – 45. Spurenworkshop in Salzburg [blooDNAcid]](https://scienceblogs.de/bloodnacid/files/2025/03/sw45.jpg)
