1920. Build Array from Permutation

1920. Build Array from Permutation

Difficulty: Easy

Topics: Array, Simulation

Given a zero-based permutation nums (0-indexed), build an array ans of the same length where ans[i] = nums[nums[i]] for each 0 <= i < nums.length and return it.

A zero-based permutation nums is an array of distinct integers from 0 to nums.length - 1 (inclusive).

Example 1:

• Input: nums = [0,2,1,5,3,4]
• Output: [0,1,2,4,5,3]
• Explanation: The array ans is built as follows:

  ans = [nums[nums[0]], nums[nums[1]], nums[nums[2]], nums[nums[3]], nums[nums[4]], nums[nums[5]]]
  = [nums[0], nums[2], nums[1], nums[5], nums[3], nums[4]]
  = [0,1,2,4,5,3]

Example 2:

• Input: nums = [5,0,1,2,3,4]
• Output: [4,5,0,1,2,3]
• Explanation: The array ans is built as follows:

  ans = [nums[nums[0]], nums[nums[1]], nums[nums[2]], nums[nums[3]], nums[nums[4]], nums[nums[5]]]
  = [nums[5], nums[0], nums[1], nums[2], nums[3], nums[4]]
  = [4,5,0,1,2,3]

Constraints:

• 1 <= nums.length <= 1000
• 0 <= nums[i] < nums.length
• The elements in nums are distinct.

Hint:

1. Just apply what's said in the statement.
2. Notice that you can't apply it on the same array directly since some elements will change after application

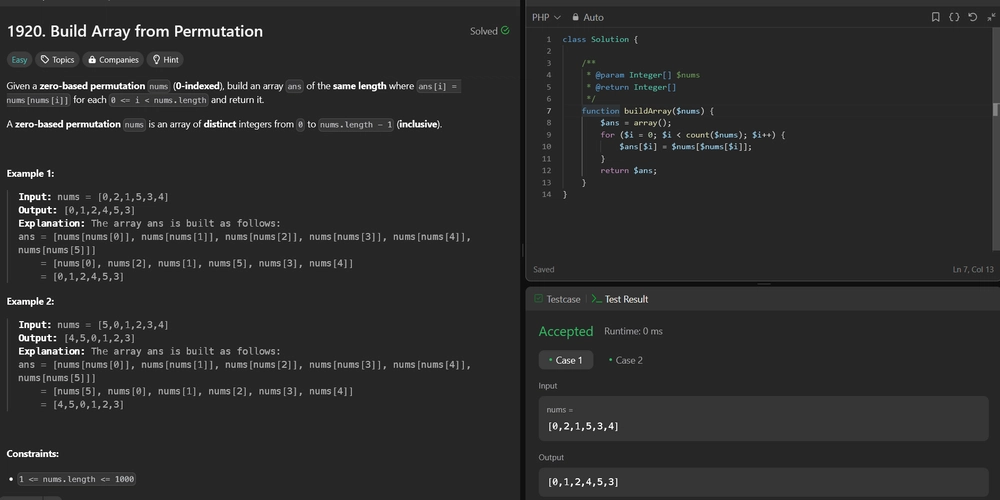
Solution:

We need to build an array ans from a given zero-based permutation nums such that each element ans[i] is equal to nums[nums[i]]. The solution involves iterating through the input array and constructing the result array using the specified transformation.

Approach

1. Problem Analysis: The problem requires transforming each element of the input array nums such that each element in the resulting array ans at index i is the element in nums at the index specified by the element in nums at index i. This can be succinctly expressed as ans[i] = nums[nums[i]].
2. Intuition: Since the input array is a zero-based permutation, each element is unique and within the valid index range. This allows us to directly use each element as an index to access another element in the same array without worrying about out-of-bounds errors.
3. Algorithm:
   • Initialize an empty array ans of the same length as nums.
   • Iterate over each index i in the input array nums.
   • For each index i, compute ans[i] as nums[nums[i]].
4. Complexity: The time complexity is O(n) where n is the length of the input array, as we iterate through the array once. The space complexity is O(n) as well, due to the storage required for the result array.

Let's implement this solution in PHP: 1920. Build Array from Permutation

/**
 * @param Integer[] $nums
 * @return Integer[]
 */
function buildArray($nums) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Test case 1
$nums1 = array(0, 2, 1, 5, 3, 4);
print_r(buildArray($nums1)); // Output: [0, 1, 2, 4, 5, 3]

// Test case 2
$nums2 = array(5, 0, 1, 2, 3, 4);
print_r(buildArray($nums2)); // Output: [4, 5, 0, 1, 2, 3]
?>

Explanation:

• Initialization: We start by creating an empty array ans to store the result.
• Iteration: We loop through each index i from 0 to the length of nums minus 1.
• Transformation: For each index i, we set ans[i] to the value of nums at the index specified by nums[i]. This effectively applies the transformation ans[i] = nums[nums[i]].
• Return: Finally, we return the constructed array ans.

This approach efficiently constructs the result array in linear time, ensuring that each element is transformed correctly according to the problem's requirements.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks