Leetcode 1007. Minimum Domino Rotations For Equal Row
Problem Statement In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the ith domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.) We may rotate the ith domino, so that tops[i] and bottoms[i] swap values. Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same. If it cannot be done, return -1. Sample Test Cases Example 1: Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2] Output: 2 Explanation: The first figure represents the dominoes as given by tops and bottoms: before we do any rotations. If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure. Example 2: Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4] Output: -1 Explanation: In this case, it is not possible to rotate the dominoes to make one row of values equal. Constraints 2 Make all bottoms elements with bottoms[0] Why does this work? Because if we can't make the first number itself equal, then we will never make the whole top or bottom dominoes with the same number. If we start rotating from the first domino, the value would be either tops[0] or bottoms[0]. This will force us to make the remaining dominoes as tops[0] or bottoms[0]. Approach Use a helper function to calculate the rotation count. We can start by checking whether tops[0] can be pushed to all the tops or bottoms. If we succeed, return the minRotation count. Otherwise, check whether the bottoms[0] can be pushed to all the tops or bottoms. Complexity Time complexity: O(length of array) Space complexity: O(1) Code class Solution { public int minDominoRotations(int[] tops, int[] bottoms) { if (tops == null || tops.length == 0 || bottoms == null || bottoms.length == 0) { return 0; } int length = tops.length; // 1. make top with tops[0] // 2. make top with bottoms[0] // 3. make bottom with tops[0] // 4. make bottom with bottoms[0] int resultWithTop = minRotation(tops[0], tops, bottoms, length); if (resultWithTop != -1) { return resultWithTop; } return tops[0] != bottoms[0] ? minRotation(bottoms[0], tops, bottoms, length) : -1; } private int minRotation(int match, int [] tops, int [] bottoms, int length) { int minRotationTop = 0; int minRotationBottom = 0; for (int index = 0; index
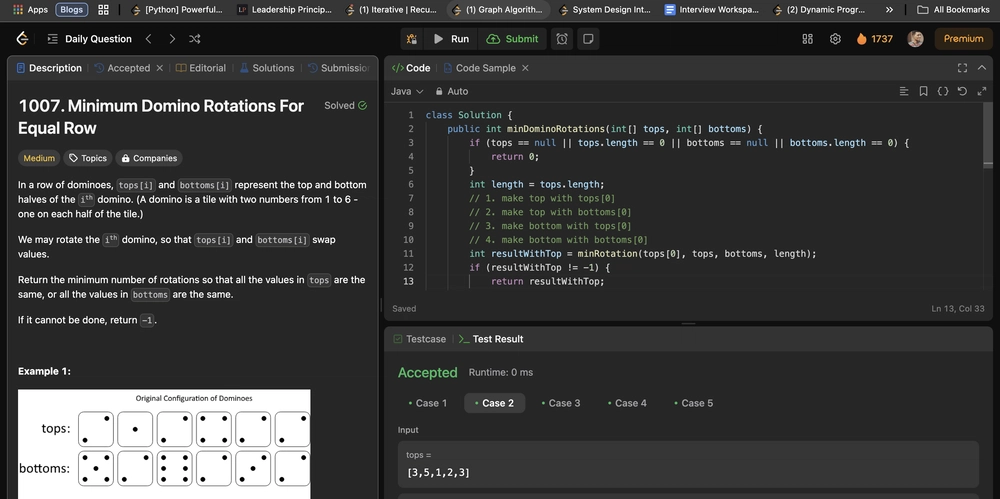
Problem Statement
In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the ith domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)
We may rotate the ith domino, so that tops[i] and bottoms[i] swap values.
Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same.
If it cannot be done, return -1.
Sample Test Cases
Example 1:
Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2]
Output: 2
Explanation:
The first figure represents the dominoes as given by tops and bottoms: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.
Example 2:
Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]
Output: -1
Explanation:
In this case, it is not possible to rotate the dominoes to make one row of values equal.
Constraints
2 <= tops.length <= 2 * 104
bottoms.length == tops.length
1 <= tops[i], bottoms[i] <= 6
Intuition
We can only make the top or bottom domino if we can make any of the 4 options.
-> Make all tops elements with tops[0]
-> Make all tops elements with bottoms[0]
-> Make all bottoms elements with top[0]
-> Make all bottoms elements with bottoms[0]
Why does this work? Because if we can't make the first number itself equal, then we will never make the whole top or bottom dominoes with the same number.
If we start rotating from the first domino, the value would be either tops[0] or bottoms[0]. This will force us to make the remaining dominoes as tops[0] or bottoms[0].
Approach
- Use a helper function to calculate the rotation count.
- We can start by checking whether tops[0] can be pushed to all the tops or bottoms.
- If we succeed, return the minRotation count.
- Otherwise, check whether the bottoms[0] can be pushed to all the tops or bottoms.
Complexity
-
Time complexity:
O(length of array)
-
Space complexity:
O(1)
Code
class Solution {
public int minDominoRotations(int[] tops, int[] bottoms) {
if (tops == null || tops.length == 0 || bottoms == null || bottoms.length == 0) {
return 0;
}
int length = tops.length;
// 1. make top with tops[0]
// 2. make top with bottoms[0]
// 3. make bottom with tops[0]
// 4. make bottom with bottoms[0]
int resultWithTop = minRotation(tops[0], tops, bottoms, length);
if (resultWithTop != -1) {
return resultWithTop;
}
return tops[0] != bottoms[0] ? minRotation(bottoms[0], tops, bottoms, length) : -1;
}
private int minRotation(int match, int [] tops, int [] bottoms, int length) {
int minRotationTop = 0;
int minRotationBottom = 0;
for (int index = 0; index < length; index++) {
if (tops[index] != match && bottoms[index] != match) {
return -1;
}
if (tops[index] != match) {
minRotationTop++;
}
else if (bottoms[index] != match) {
minRotationBottom++;
}
}
return Math.min(minRotationTop, minRotationBottom);
}
}