ECDSA: What You Need to Know About This Cryptographic Workhorse

Look, I've been working with cryptography for years now, and if there's one thing that keeps coming up in my projects, it's ECDSA. Frankly, I was confused as hell about it at first - all this talk of elliptic curves and finite fields made my head spin. But after implementing it in several projects (and debugging some nightmare scenarios), I've grown to appreciate this clever bit of math.

So let's break down ECDSA without getting lost in a forest of equations, shall we?

What is Elliptic Curve Digital Signature Algorithm (ECDSA) anyway?

ECDSA stands for Elliptic Curve Digital Signature Algorithm. I know, I know - it's a mouthful. But here's what you actually need to know: it's basically a way to prove you have a secret (your private key) without revealing that secret.

Think of it like proving you know the password to your email without actually typing your password where someone could see it. Pretty neat trick, right?

The "Elliptic Curve" part refers to the specific mathematical structure it's built on. Trust me when I say we don't need to dive into the actual math here (unless you really want to fall down that rabbit hole). The important thing is that these curves give us strong security with much smaller numbers than older methods like RSA.

Why should you care about ECDSA?

Well, if you've used Bitcoin or pretty much any other cryptocurrency, ECDSA is what prevents someone from stealing your coins. It's also securing a ton of the websites you visit daily.

But what makes it special compared to older stuff like RSA?

It's WAY more compact: An ECDSA key that's just 256 bits long is roughly as secure as an RSA key that's 3072 bits. That's a huge difference!

It's faster: Especially on devices where processing power matters (like your phone)

It uses less bandwidth: Smaller signatures mean less data to transmit

I remember working on an IoT project where we had to switch from RSA to ECDSA because the devices were too constrained. The difference was night and day - suddenly our battery life improved dramatically and communication delays dropped.

How ECDSA works (the non-headache version)

I'll spare you the complex math, but here's the basic flow:

1. You generate your keys

• Your private key is basically just a really big random number
• Your public key is derived from that through some elliptic curve magic
• You keep the private key secret and share the public key freely

2. To sign something:

• You take whatever you're signing and run it through a hash function
• You combine this hash with your private key and a fresh random number
• Out pops a signature (two numbers that we call r and s)

3. Someone else verifies your signature:

• They take your public key and do some math with your signature
• If everything checks out, they know You must have signed it
• If even a single bit of the original message changed, verification fails

The beauty is in the details, but this is the gist. And honestly, unless you're implementing the algorithm yourself (please don't unless you really know what you're doing), this level of understanding is sufficient.

Where you'll find ECDSA in the wild

This stuff is everywhere once you know what to look for:

Bitcoin & cryptocurrencies: Every transaction is signed with ECDSA
HTTPS websites: Lots of TLS certificates use ECDSA these days
Mobile apps: Especially for secure communication
VPNs: Many use ECDSA for authentication
SSH keys: The newer ed25519 keys are based on similar elliptic curve principles

I still remember the first time I generated a Bitcoin wallet. It felt like magic that this mathematical algorithm could secure potentially millions of dollars with just a tiny key. But that's the power of modern cryptography.

The scary parts nobody talks about enough

Here's the thing - ECDSA is secure IN THEORY. But holy hell, the implementation details matter.

Back in 2010, Sony messed up their PlayStation 3 implementation of ECDSA by using the same "random" number for every signature. Game over. The entire security system collapsed.

Similar mistakes have led to Bitcoin thefts. This stuff isn't theoretical - real money has been lost because of implementation errors.

If you're implementing ECDSA yourself, please:

• Use a cryptographically secure random number generator
• NEVER reuse the "k" value (the random number used in signing)
• Be aware of side-channel attacks (timing attacks, power analysis, etc.)
• Don't roll your own crypto if you can avoid it

How ECDSA stacks up against the competition

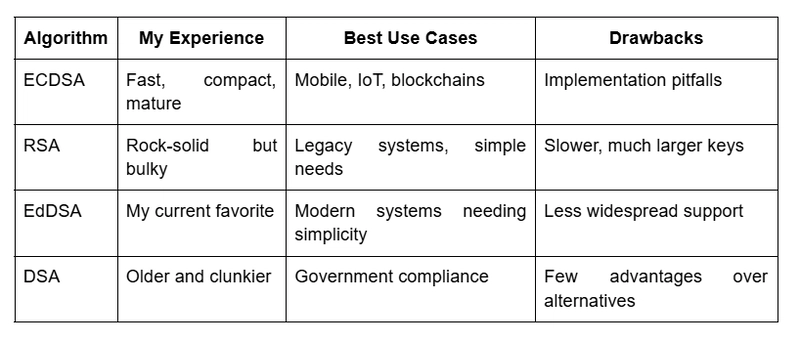
I've worked with several signature algorithms over the years. Here's my take:

I've mostly switched to EdDSA (specifically Ed25519) for new projects when I can. It addresses some of ECDSA's implementation pitfalls while keeping the benefits. But ECDSA is still incredibly widespread. You can also refer to this article Diffie-Hellman, RSA, DSA, ECC and ECDSA –Algorithms for more details.

Looking forward: The quantum threat

I worry about quantum computing's impact on all this. When (not if) large-scale quantum computers arrive, ECDSA will be broken. So will RSA and pretty much all our current public key crypto.

The industry is working on "post-quantum" algorithms, but we're in this awkward in-between period. I'm keeping an eye on NIST's standardization process, but for now, ECDSA remains secure against classical computers.

Final thoughts

After years working with this stuff, I've developed a healthy respect for ECDSA. It's not perfect - nothing in security is - but it represents a clever balance of security and efficiency.

If you're building systems that need digital signatures, ECDSA is usually a solid choice - just make sure you're using a well-tested library rather than implementing it yourself. Your future self (and your users) will thank you.

_Learned something useful from this article? I'm always improving my explanations, so drop a comment with questions or share your own experiences with cryptographic algorithms. I'm particularly interested in hearing about any strange ECDSA implementation issues you've encountered!
_