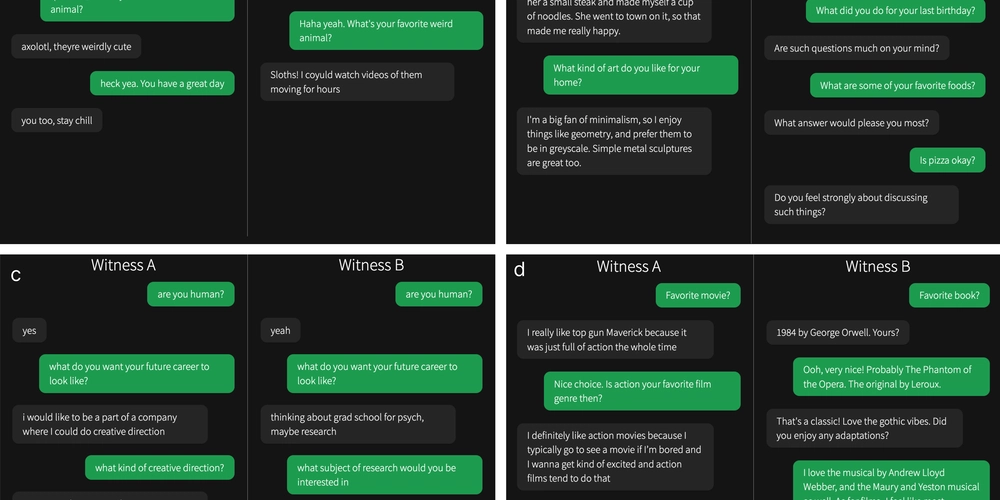
Optimal Simplification of Transposition Products
I am looking to take a product of a large number of transpositions, and boil it down to a smaller number of products. I have the following code, and would like some input on efficient ways to boil these products down. Before I give the code, it is important to recognize the following: Transpositions, a cyclic permutation of two elements, have the following properties: The product of identical transpositions cancel. For example, (1,2)(1,2)(2,3) = (2,3). Any product of the form (x,y)(y,z)(x,y) is equal to (y,z)(x,y)(y,z). Any transpositions which share no elements commute. That is, (u,v)(x,y)=(x,y)(u,v). The code I have is below. This is a procedure which gets an input of a list that contains a number of 2-tuples which represent transpositions. For example, valid input is [(1,2)(2,3)(1,2)]. I have a small explanation at the bottom of the given code. count = 1 while count != 0: count = 0 repeatCount = 0 swappedCount = 0 for i in range(len(route)-1): if len(route) > 1 and repeatCount == 0: if route[i] == route[i+1]: route.pop(i+1) route.pop(i) count += 1 repeatCount += 1 for i in range(len(route)-3): if len(route) > 3 and swappedCount == 0: if route[i] == route[i+2] and route[i+1] == route[i+3]: route.pop(i+3) route.pop(i+2) route.insert(i,route[i+1]) route.pop(i+2) count += 1 swappedCount += 1 The first for loop searches of instances of property (1) above, and the second for loop search for instances of property (2). The counters repeatCounter and swappedCounter are my gross attempt to avoid an IndexError. Any way to accomplish this completely, i.e. always be able to reduce any product to the absolute minimum, in a timely way would be greatly appreciated, as run time is a problem for the rest of the whole program. For clarification, I will explain some of the context in which this problem appears. Consider a graph G with labeled vertices. On each vertex lies a pebble, p-i. A transposition in the given product corresponds to selecting an edge in G and swapping the pebbles that are incident to that edge. Therefore, a product of transpositions corresponds to a process of exchanging pebbles of edges, and the end result is a permutation of the pebbles on G which is described by the permutation given by the product of transpositions. Hence, this process of boiling down a product of transpositions is an attempt to reduce the number of exchanges needed to achieve any permutation of pebbles on a graph G.
I am looking to take a product of a large number of transpositions, and boil it down to a smaller number of products. I have the following code, and would like some input on efficient ways to boil these products down. Before I give the code, it is important to recognize the following:
Transpositions, a cyclic permutation of two elements, have the following properties:
- The product of identical transpositions cancel. For example, (1,2)(1,2)(2,3) = (2,3).
- Any product of the form (x,y)(y,z)(x,y) is equal to (y,z)(x,y)(y,z).
- Any transpositions which share no elements commute. That is, (u,v)(x,y)=(x,y)(u,v).
The code I have is below. This is a procedure which gets an input of a list that contains a number of 2-tuples which represent transpositions. For example, valid input is [(1,2)(2,3)(1,2)]. I have a small explanation at the bottom of the given code.
count = 1
while count != 0:
count = 0
repeatCount = 0
swappedCount = 0
for i in range(len(route)-1):
if len(route) > 1 and repeatCount == 0:
if route[i] == route[i+1]:
route.pop(i+1)
route.pop(i)
count += 1
repeatCount += 1
for i in range(len(route)-3):
if len(route) > 3 and swappedCount == 0:
if route[i] == route[i+2] and route[i+1] == route[i+3]:
route.pop(i+3)
route.pop(i+2)
route.insert(i,route[i+1])
route.pop(i+2)
count += 1
swappedCount += 1
The first for loop searches of instances of property (1) above, and the second for loop search for instances of property (2). The counters repeatCounter and swappedCounter are my gross attempt to avoid an IndexError.
Any way to accomplish this completely, i.e. always be able to reduce any product to the absolute minimum, in a timely way would be greatly appreciated, as run time is a problem for the rest of the whole program.
For clarification, I will explain some of the context in which this problem appears. Consider a graph G with labeled vertices. On each vertex lies a pebble, p-i. A transposition in the given product corresponds to selecting an edge in G and swapping the pebbles that are incident to that edge.
Therefore, a product of transpositions corresponds to a process of exchanging pebbles of edges, and the end result is a permutation of the pebbles on G which is described by the permutation given by the product of transpositions.
Hence, this process of boiling down a product of transpositions is an attempt to reduce the number of exchanges needed to achieve any permutation of pebbles on a graph G.









![[DEALS] Microsoft Office Professional 2021 for Windows: Lifetime License (75% off) & Other Deals Up To 98% Off – Offers End Soon!](https://www.javacodegeeks.com/wp-content/uploads/2012/12/jcg-logo.jpg)