Merge Sort
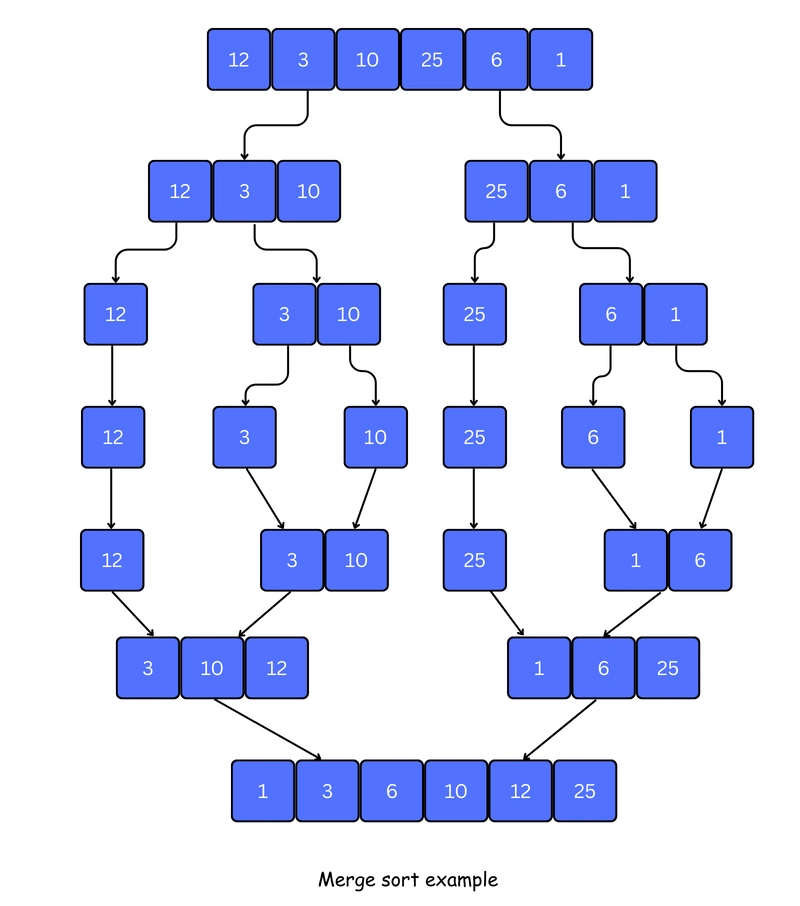
Merge Sort is one of the most popular sorting algorithms that is based on the principle of Divide and Conquer Algorithm. In this approach, the problem is broken down into smaller sub-problems, each of which is solved separately. The solutions to these sub-problems are then combined to form the final solution. Working of Merge Sort Suppose we need to sort the following array. 1. Find the Midpoint Divide the array into two halves by calculating the middle index. 2. Split into Left and Right Arrays Create a left array with elements before the mid. Create a right array with elements from mid to the end. 3. As we know javascript is synchronous so, recursively call mergeSort() on left Array This process is for first left array which we inserted initially and further process for first right array can see in step 7. so, Keep dividing the left array until each sub-array contains only one element. Steps 1 and 2 will repeat during this process. 4. Recursively Call mergeSort() on right Array Repeat the same process for the right array — divide and reduce to single elements. Steps 1 and 2 will repeat during this process. 5. Merge and sort left and right array by calling merge() function When both left and right return single-element arrays, the merge() function is called to combine and sort them. 6. Repeat Merging Up the Stack The merge() function continues to be called step-by-step as the recursion unwinds, combining and sorting the small arrays until the full array is rebuilt and sorted. In below image we taken the left array of step 3 and right array of step 5. 7. Now we recursively call mergeSort() function for the first right array which we inserted in step 1 for that we again follow the same process of step 1 and step 2 8. Again we recursively call mergeSort() function. 9. Merge left and right Array. 10. Again Merge and sort left and right array. 11. finally we merge and sort left and right array of step 6 and step 10. Merge Sort Algorithm function MERGE_SORT(array) if length of array ≤ 1 return array mid ← floor(length of array / 2) left ← empty array right ← empty array for i from 0 to mid - 1 add array[i] to left for i from mid to length of array - 1 add array[i] to right left ← MERGE_SORT(left) right ← MERGE_SORT(right) return MERGE(left, right) function MERGE(left, right) result ← empty array i ← 0 j ← 0 while i a.price - b.price); 2. Leaderboard Ranking System
Merge Sort is one of the most popular sorting algorithms that is based on the principle of Divide and Conquer Algorithm.
In this approach, the problem is broken down into smaller sub-problems, each of which is solved separately. The solutions to these sub-problems are then combined to form the final solution.
Working of Merge Sort
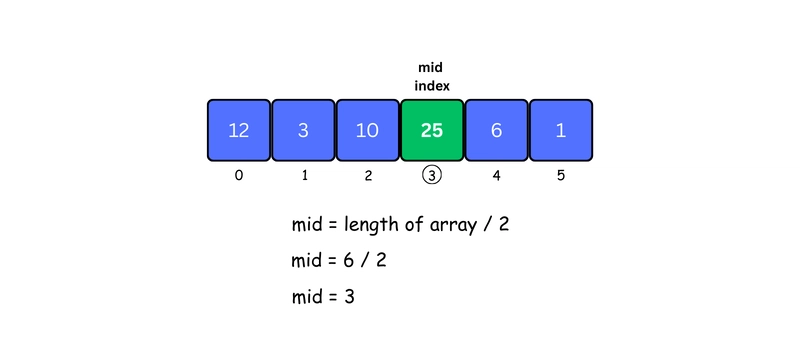
Suppose we need to sort the following array.
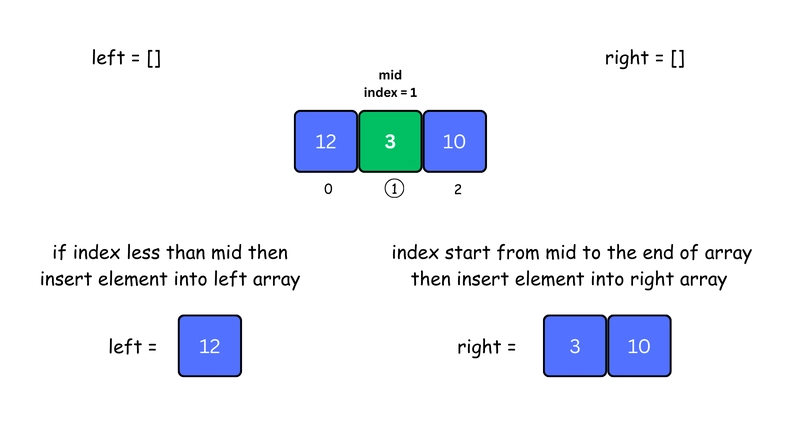
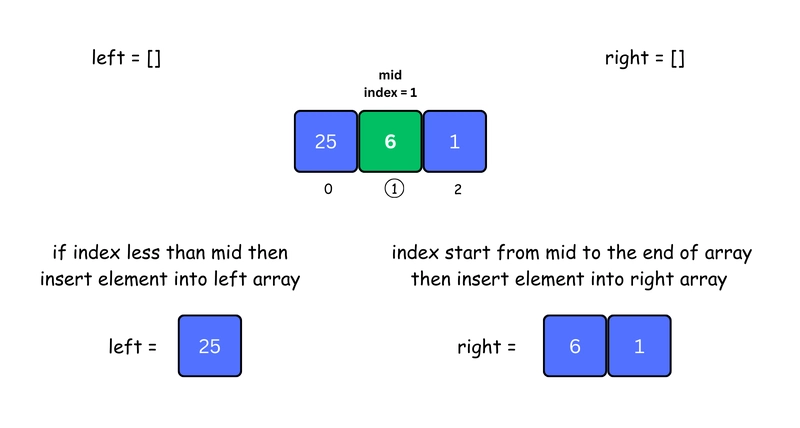
1. Find the Midpoint
Divide the array into two halves by calculating the middle index.
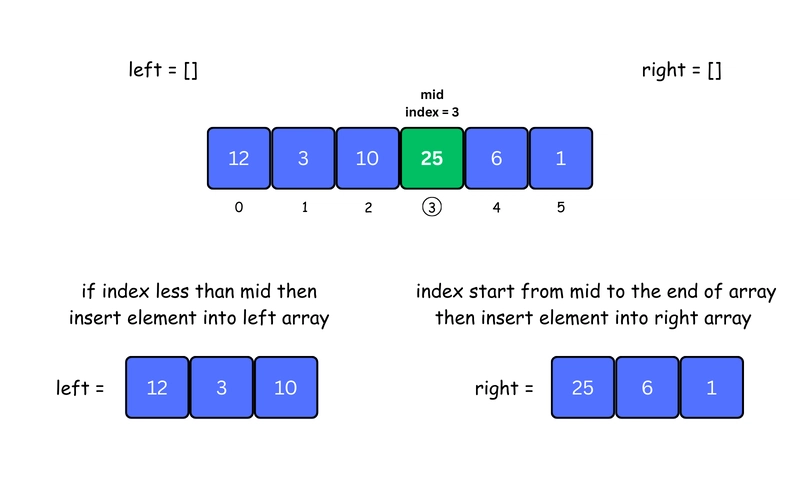
2. Split into Left and Right Arrays
Create a
leftarray with elements before themid.Create a
rightarray with elements frommidto the end.
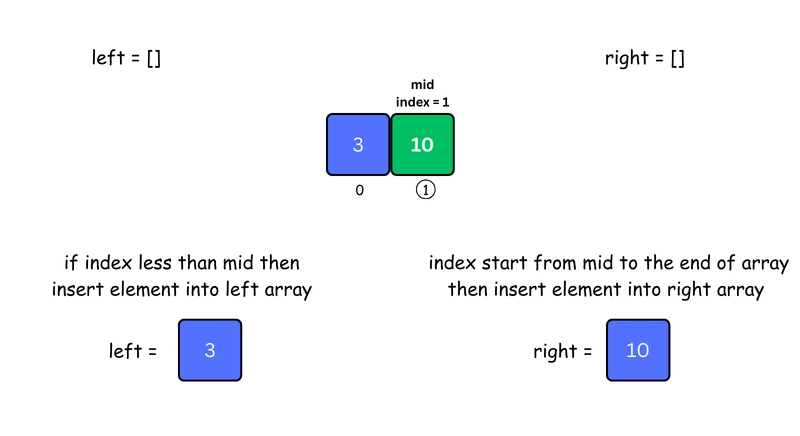
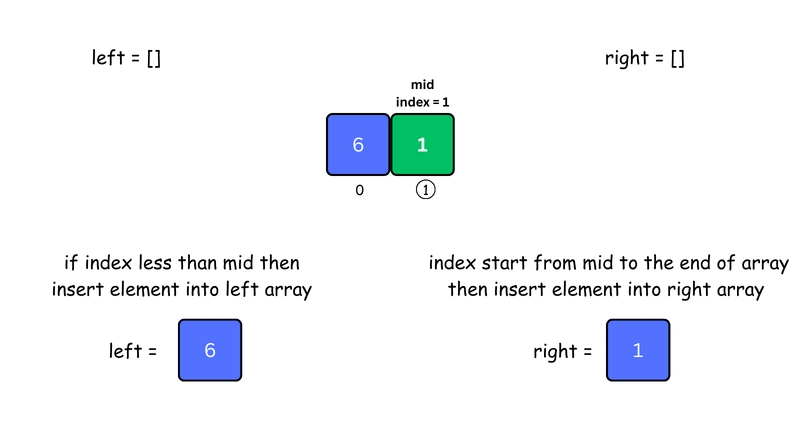
3. As we know javascript is synchronous so, recursively call mergeSort() on left Array
This process is for first left array which we inserted initially and further process for first right array can see in step 7. so, Keep dividing the left array until each sub-array contains only one element. Steps 1 and 2 will repeat during this process.
4. Recursively Call mergeSort() on right Array
Repeat the same process for the right array — divide and reduce to single elements. Steps 1 and 2 will repeat during this process.
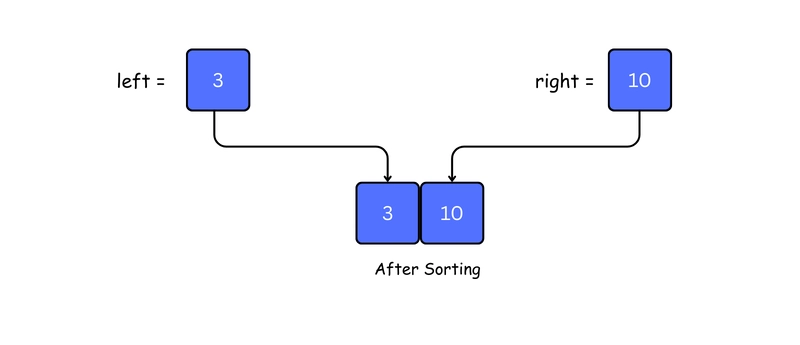
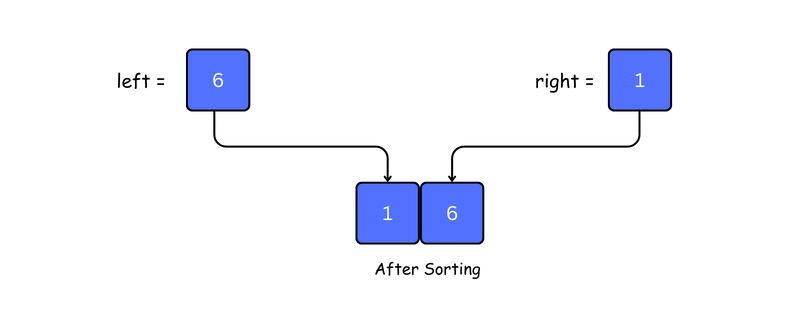
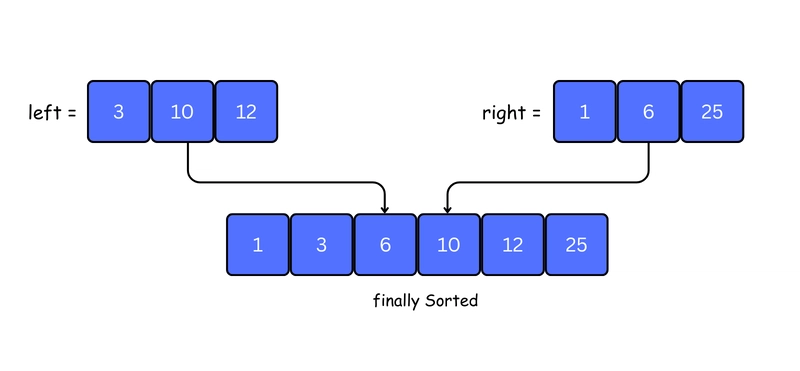
5. Merge and sort left and right array by calling merge() function
When both left and right return single-element arrays, the merge() function is called to combine and sort them.
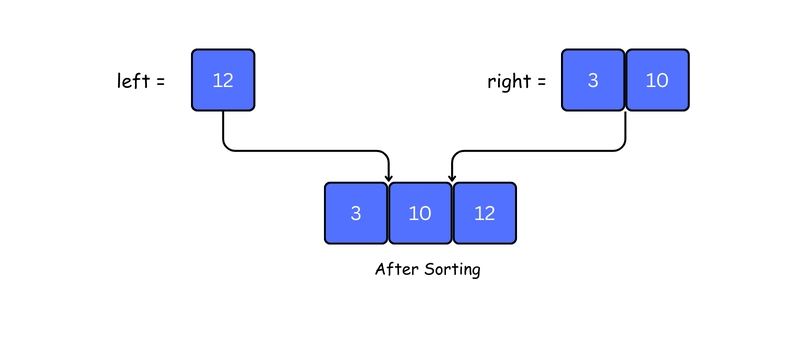
6. Repeat Merging Up the Stack
The merge() function continues to be called step-by-step as the recursion unwinds, combining and sorting the small arrays until the full array is rebuilt and sorted.
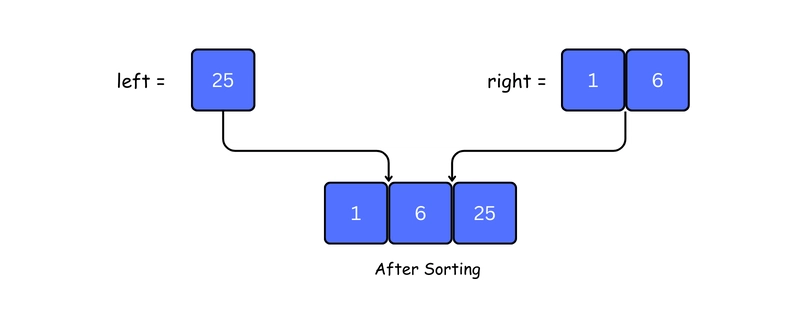
In below image we taken the left array of step 3 and right array of step 5.
7. Now we recursively call mergeSort() function for the first right array which we inserted in step 1 for that we again follow the same process of step 1 and step 2
8. Again we recursively call mergeSort() function.
9. Merge left and right Array.
10. Again Merge and sort left and right array.
11. finally we merge and sort left and right array of step 6 and step 10.
Merge Sort Algorithm
function MERGE_SORT(array)
if length of array ≤ 1
return array
mid ← floor(length of array / 2)
left ← empty array
right ← empty array
for i from 0 to mid - 1
add array[i] to left
for i from mid to length of array - 1
add array[i] to right
left ← MERGE_SORT(left)
right ← MERGE_SORT(right)
return MERGE(left, right)
function MERGE(left, right)
result ← empty array
i ← 0
j ← 0
while i < length of left AND j < length of right
if left[i] < right[j]
append left[i] to result
i ← i + 1
else
append right[j] to result
j ← j + 1
while i < length of left
append left[i] to result
i ← i + 1
while j < length of right
append right[j] to result
j ← j + 1
return result
Merge Sort Code
function mergeSort(arr) {
if (arr.length <= 1) return arr;
let mid = Math.floor(arr.length / 2);
let left = [];
let right = [];
for (let i = 0; i < mid; i++) left[left.length] = arr[i];
for (let i = mid; i < arr.length; i++) right[right.length] = arr[i];
left = mergeSort(left);
right = mergeSort(right);
return merge(left, right);
}
function merge(left, right) {
let result = [];
let i = 0,
j = 0;
while (i < left.length && j < right.length) {
if (left[i] < right[j]) {
result[result.length] = left[i];
i++;
} else {
result[result.length] = right[j];
j++;
}
}
while (i < left.length){
result[result.length] = left[i];
i++;
}
while (j < right.length){
result[result.length] = right[j];
j++;
}
return result;
}
console.log(mergeSort([12, 3, 10, 25, 6, 1]));
Merge Sort Complexity
| Time Complexity | |
|---|---|
| Best | O(n*log n) |
| Worst | O(n*log n) |
| Average | O(n*log n) |
| Space Complexity | O(n) |
| Stability | Yes |
1. Time Complexities
Worst Case Complexity: O(n log n)
Merge Sort always divides the array into two halves and takes linear time to merge two halves. The division happens log n times and merging takes O(n) time, resulting in O(n log n) overall.Best Case Complexity: O(n log n)
Even when the array is already sorted, Merge Sort still divides and merges the array the same way, so the best case is also O(n log n).Average Case Complexity: O(n log n)
On average, Merge Sort performs consistently in O(n log n) time due to the divide-and-conquer approach.
2. Space Complexity
- Space Complexity: O(n) Merge Sort requires additional space proportional to the size of the array for merging the divided arrays. So, the auxiliary space used is O(n).
Real-World Application of Merge Sort
1. E-Commerce Product Sorting