Celebrating World Quantum Day: Advancing Quantum State Tomography with Physics-Informed Neural Networks
Today, on World Quantum Day, I’m excited to share a breakthrough in quantum state tomography (QST) using physics-informed neural networks (PINNs). This new approach simplifies the complex task of reconstructing quantum states, a critical process in quantum computing, and offers promising implications for the field. Quantum state tomography is like taking a detailed snapshot of a quantum system. It involves measuring a quantum state—such as the state of particles in a quantum computer—and reconstructing a mathematical description called a density matrix. This matrix tells us everything about the state, including its probabilities and behaviors. Traditional methods for QST, like maximum likelihood estimation, struggle with large systems and are sensitive to measurement noise, making them inefficient as quantum computers grow in size. Our method uses a PINN, a type of neural network that embeds the rules of quantum physics directly into its learning process. We designed a network with five hidden layers, each containing 512 neurons, to map measurement data from a 2-qubit system to a density matrix. For a 2-qubit system, this matrix is 4x4, and we ensure it follows quantum rules: it must be Hermitian (a symmetry property), have a trace of 1 (a normalization rule), and be positive semi-definite (ensuring physical validity). These constraints are enforced through the network’s loss function and post-processing steps, making the output a valid quantum state. We trained the PINN on a dataset of 500 synthetic 2-qubit quantum states, each with corresponding measurement outcomes. The training process optimized a loss function that balances data accuracy with physical constraints, such as penalizing negative eigenvalues to ensure the density matrix is valid. After 10 epochs, the model converged with a low error, achieving a test set mean squared error of 0.0061. The results are encouraging. Across 500 test states, our method achieved an average fidelity of 0.8752, meaning the reconstructed states are 87.52% similar to the true states. Fidelity measures how close two quantum states are, with 1 being identical. We also measured a trace distance of 0.2499, which indicates how distinguishable the reconstructed state is from the true state (lower is better), and a purity of 1.0012, slightly above the ideal value of 1 for pure states due to numerical precision but still indicating high quality. What does this mean for quantum computing? First, our approach is more scalable than traditional QST methods, handling larger systems more efficiently. This is crucial as quantum computers grow in qubit count, where traditional methods become computationally infeasible. Second, it’s robust to noise, producing valid quantum states even with imperfect measurements—a common challenge in real quantum hardware. Finally, we used SHAP analysis to interpret the model, revealing which features (like fidelity and purity) most influence the reconstruction, offering insights that traditional methods can’t provide. For the broader field of quantum computing, this work paves the way for more reliable and efficient characterization of quantum states. As quantum computers advance, tools like this will be essential for debugging, validating, and optimizing quantum algorithms. Our next steps involve scaling to larger systems and integrating adaptive measurement strategies to further boost performance. On this World Quantum Day, this PINN-based QST method highlights how AI can accelerate quantum research, bringing us closer to practical, large-scale quantum computing solutions. Let’s keep pushing the boundaries of what’s possible in quantum technology. link to the kaggle notebook: https://www.kaggle.com/code/allanwandia/pinn-s-qst
Today, on World Quantum Day, I’m excited to share a breakthrough in quantum state tomography (QST) using physics-informed neural networks (PINNs). This new approach simplifies the complex task of reconstructing quantum states, a critical process in quantum computing, and offers promising implications for the field.
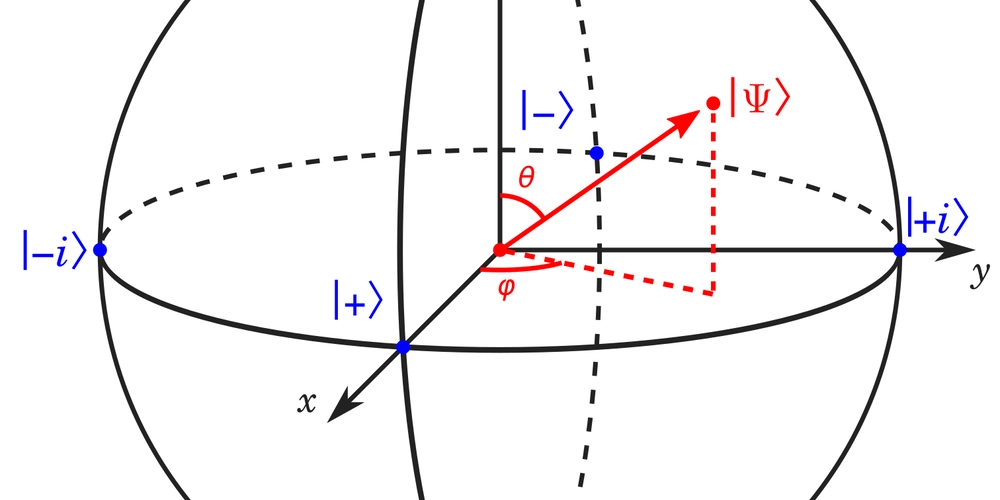
Quantum state tomography is like taking a detailed snapshot of a quantum system. It involves measuring a quantum state—such as the state of particles in a quantum computer—and reconstructing a mathematical description called a density matrix. This matrix tells us everything about the state, including its probabilities and behaviors. Traditional methods for QST, like maximum likelihood estimation, struggle with large systems and are sensitive to measurement noise, making them inefficient as quantum computers grow in size.
Our method uses a PINN, a type of neural network that embeds the rules of quantum physics directly into its learning process. We designed a network with five hidden layers, each containing 512 neurons, to map measurement data from a 2-qubit system to a density matrix. For a 2-qubit system, this matrix is 4x4, and we ensure it follows quantum rules: it must be Hermitian (a symmetry property), have a trace of 1 (a normalization rule), and be positive semi-definite (ensuring physical validity). These constraints are enforced through the network’s loss function and post-processing steps, making the output a valid quantum state.
We trained the PINN on a dataset of 500 synthetic 2-qubit quantum states, each with corresponding measurement outcomes. The training process optimized a loss function that balances data accuracy with physical constraints, such as penalizing negative eigenvalues to ensure the density matrix is valid. After 10 epochs, the model converged with a low error, achieving a test set mean squared error of 0.0061.
The results are encouraging. Across 500 test states, our method achieved an average fidelity of 0.8752, meaning the reconstructed states are 87.52% similar to the true states. Fidelity measures how close two quantum states are, with 1 being identical. We also measured a trace distance of 0.2499, which indicates how distinguishable the reconstructed state is from the true state (lower is better), and a purity of 1.0012, slightly above the ideal value of 1 for pure states due to numerical precision but still indicating high quality.
What does this mean for quantum computing? First, our approach is more scalable than traditional QST methods, handling larger systems more efficiently. This is crucial as quantum computers grow in qubit count, where traditional methods become computationally infeasible. Second, it’s robust to noise, producing valid quantum states even with imperfect measurements—a common challenge in real quantum hardware. Finally, we used SHAP analysis to interpret the model, revealing which features (like fidelity and purity) most influence the reconstruction, offering insights that traditional methods can’t provide.
For the broader field of quantum computing, this work paves the way for more reliable and efficient characterization of quantum states. As quantum computers advance, tools like this will be essential for debugging, validating, and optimizing quantum algorithms. Our next steps involve scaling to larger systems and integrating adaptive measurement strategies to further boost performance.
On this World Quantum Day, this PINN-based QST method highlights how AI can accelerate quantum research, bringing us closer to practical, large-scale quantum computing solutions. Let’s keep pushing the boundaries of what’s possible in quantum technology.
link to the kaggle notebook: https://www.kaggle.com/code/allanwandia/pinn-s-qst