2873. Maximum Value of an Ordered Triplet I

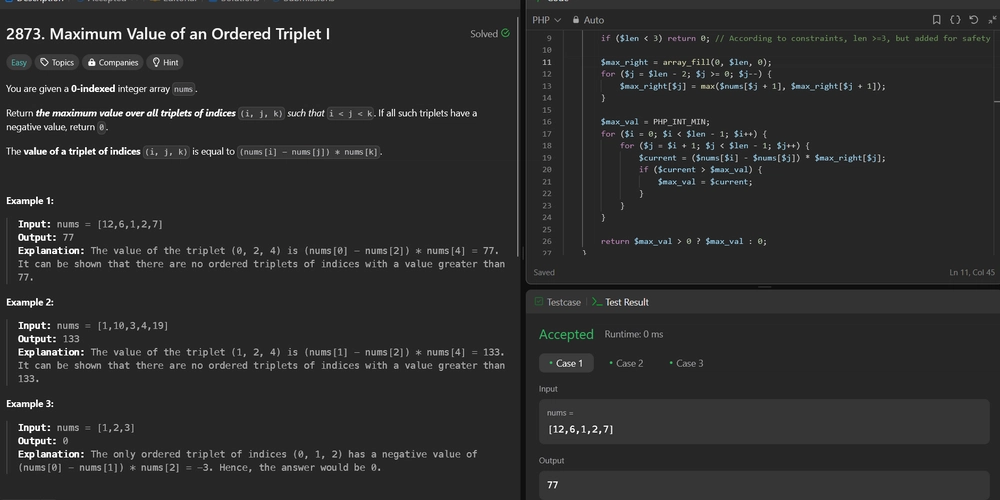
2873. Maximum Value of an Ordered Triplet I

Difficulty: Easy

Topics: Array

You are given a 0-indexed integer array nums.

Return the maximum value over all triplets of indices (i, j, k) such that i < j < k. If all such triplets have a negative value, return 0.

The value of a triplet of indices (i, j, k) is equal to (nums[i] - nums[j]) * nums[k].

Example 1:

• Input: nums = [12,6,1,2,7]
• Output: 77
• Explanation: The value of the triplet (0, 2, 4) is (nums[0] - nums[2]) * nums[4] = 77.
  • It can be shown that there are no ordered triplets of indices with a value greater than 77.

Example 2:

• Input: nums = [1,10,3,4,19]
• Output: 133
• Explanation: The value of the triplet (1, 2, 4) is (nums[1] - nums[2]) * nums[4] = 133.
  • It can be shown that there are no ordered triplets of indices with a value greater than 133.

Example 3:

• Input: nums = [1,2,3]
• Output: 0
• Explanation: The only ordered triplet of indices (0, 1, 2) has a negative value of (nums[0] - nums[1]) * nums[2] = -3. Hence, the answer would be 0.

Constraints:

• 3 <= nums.length <= 100
• 1 <= nums[i] <= 106

Hint:

1. Use three nested loops to find all the triplets.

Solution:

We need to find the maximum value of all possible ordered triplets (i, j, k) such that i < j < k in a given array. The value of each triplet is calculated as (nums[i] - nums[j]) * nums[k]. If all such triplets have a negative value, we return 0.

Approach

The key insight to optimize the solution is to recognize that for each pair (i, j), the maximum possible value of the triplet (i, j, k) can be determined by the maximum value of nums[k] for k > j. This allows us to precompute the maximum value to the right of each index j, which reduces the problem from O(n^3) time complexity to O(n^2).

1. Precompute Maximum Values: Create an array max_right where each element at index j is the maximum value of nums from index j+1 to the end of the array. This helps in quickly determining the maximum possible nums[k] for any given j.
2. Iterate Over Pairs (i, j): For each valid pair (i, j) where i < j, compute the value using the precomputed max_right array to find the maximum possible value of the triplet (i, j, k) efficiently.
3. Determine Result: Track the maximum value obtained from all valid triplets. If the maximum value is non-positive, return 0; otherwise, return the maximum value.

Let's implement this solution in PHP: 2873. Maximum Value of an Ordered Triplet I

/**
 * @param Integer[] $nums
 * @return Integer
 */
function maximumTripletValue($nums) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Test cases
$nums1 = [12,6,1,2,7];
$nums2 = [1,10,3,4,19];
$nums3 = [1,2,3];

echo maximumTripletValue($nums1) . "\n"; // Output: 77
echo maximumTripletValue($nums2) . "\n"; // Output: 133
echo maximumTripletValue($nums3) . "\n"; // Output: 0
?>

Explanation:

1. Precompute Maximum Values: The max_right array is constructed by iterating from the end of the array to the start. For each index j, max_right[j] stores the maximum value of the subarray starting from j+1 to the end. This allows O(1) access to the maximum possible nums[k] for any j.
2. Iterate Over Pairs (i, j): For each pair (i, j), the value of the triplet is calculated using the precomputed maximum value from max_right[j]. This avoids the need to iterate over k explicitly, reducing the time complexity.
3. Result Calculation: The maximum value obtained from all valid pairs (i, j) is checked. If it is positive, it is returned; otherwise, 0 is returned, ensuring we handle the case where all triplet values are non-positive efficiently.

This approach efficiently reduces the problem complexity by leveraging precomputed values, making it feasible to handle larger input sizes within acceptable time limits.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks